This post speaks to a mathematical refinement in evaluating the performance of a portfolio of heat pumps — the difference between portfolio SCOP and the average of individual SCOPs across a portfolio — a refinement that may or may not be important in the real world. We will only get a better sense whether this distinction is important if more and more cold-climate efficiency agencies (Mass Save and its counterparts in other northern states and countries) complete high quality evaluations of their programs.
If Mass Save incentives lead to the installation of 100,000 heat pumps, then from a climate perspective one would really want to know the overall seasonal coefficient of performance of the portfolio of installations. In other words, to understand overall impact, one would be most interested in the following ratio: the total of heat energy provided by all pumps divided by the total electrical energy used by all the pumps. Let’s call that quantity SCOPPortfolio.
SCOPPortfolio could be the same as the average of the individual SCOPs for each of the pumps and the benefit-cost models used by Mass Save effectively assume these quantities to be the same. But they could also be different. We know that real world heat pumps installations vary both in their annual load and their SCOP. The examples below show that total seasonal power demand could be different for collections of pumps serving the same total heating load with the same average of individual SCOPs. In other words, the SCOPPortfolio. could vary across collections of pump with the same average of individual SCOPs.
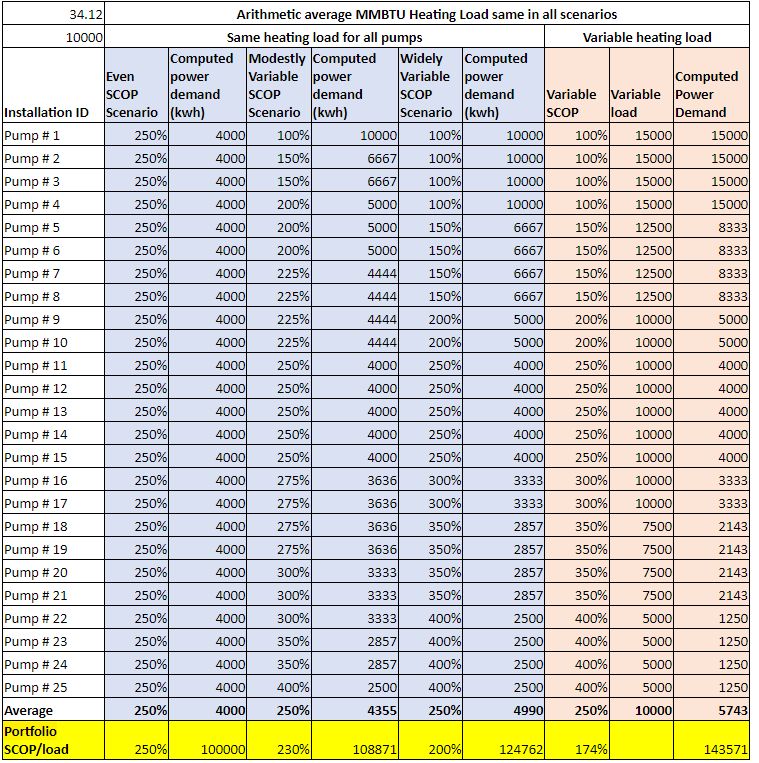
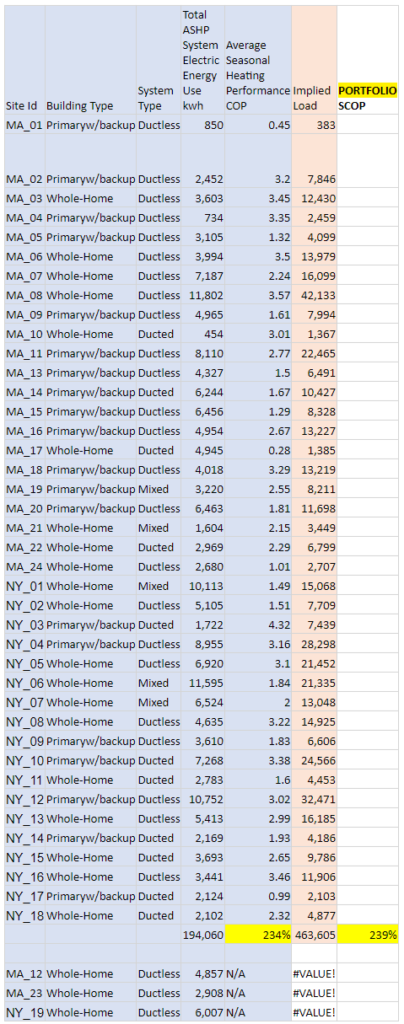
As a generalization, one might expect that, as in these examples, the SCOPPortfolio would be lower than the average of the pump SCOPs, because less efficient pumps will have a greater impact on the portfolio performance than more efficient pumps serving the same load. However, it could go either way, depending on the mix of individual loads and SCOPs. The example below, from a real-world collection of pumps studied for the MassCEC (see slides 100 to 105), shows the numbers coming out roughly the same.,