View my November 1 zoom discussion of Senate Redistricting here. This discussion includes an overview of the process, key concepts of redistricting and review of my new district.
I posted this note originally on October 12. I have revised the district description and graphics to reflect plan revisions through October 19. I have also included graphics which may be more legible.
Every ten years, following the decennial census, the legislature has to redraw its districts.
As Senate Co-Chair of the Special Joint Committee on Redistricting, it has been my charge to understand the relevant law and data and to conduct a fair and transparent process to redraw the 40 state senate districts.
I have spent much of the past few years and almost every waking hour over the past few months working on this project. I have been guided and assisted by a great staff, superb lawyers, a brilliant statistician, many respected colleagues, many respected outside advocates (notably, The New Democracy Coalition and The Drawing Democracy Coalition), and, most importantly, by broad public input.
Today, we rolled out the results of that process in draft form. Materials on the new districts statewide may be found on our committee website. The Globe is also giving the process thorough coverage. My video overview of the issues in the senate map appears at this link, at approximately 41 minutes in.
The district that I serve is currently referred to as the Second Suffolk and Middlesex and is numbered D28 in the proposed plan. The proposed plan would:
- Consolidate Allston and Brighton fully into D28 — currently, I represent most of these communities, but North Allston is under Senator DiDomenico.
- Add most of West Cambridge to D28.
- Remove the South End, most of the Back Bay and some of the East Fens from D28.
- Keep the West Fens and much of the East Fens in D28 — I would stay engaged with Charlesgate and Fenway concerns.
- Keep Belmont and Watertown in D28.
I love all parts of my existing district and treasure my friends in all parts of my existing district. As chair, I have attempted to limit the role of my personal feelings in the decision-making process. These changes are all driven by a combination of demographic shifts in the Boston area — both as to total population within neighborhoods and as to voting rights issues for minority groups — and by traditional redistricting considerations such as compactness and simplicity.
Here is the revised map, voted by the Joint Redistricting Committee, as of October 19. My District is D28. This map is still subject to change by vote on the Senate floor, but represents the final vote of the committee after extensive input. In particular, this map reflects boundary changes to harmonize with the House map and the City of Boston’s proposed new precincts.

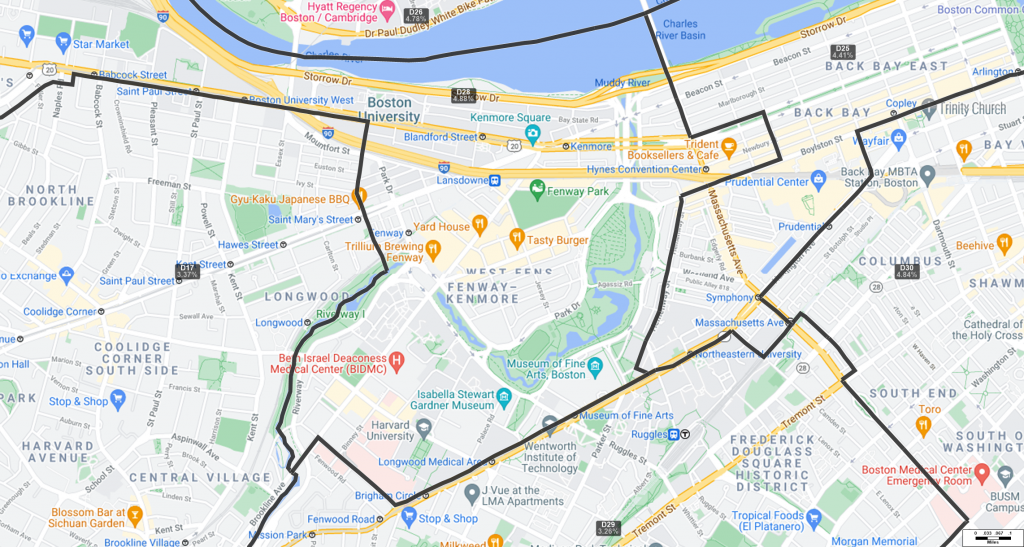
The map below shows the detail for the boundary of D28 in the Fenway neighborhood.

Will, I have really enjoyed working with you and appreciate all you have done while representing Back Bay. I hope that our paths will continue to cross.
Im glad you’ll still be representing me. Thanks for all you do.
I think this is called gerrymandering and is supposed to be a big no-no.
I suppose it depends on who is doing the gerrymandering and whether the Boston Globe approves or not since it controls the narrative.
Pasting this link here for no particular reason:
https://chrome.google.com/webstore/detail/willbrownsbergercom-filte/ocddkabnknofagjjbpdhncbgkcfmhbpd
Thank you Jonathan! This is a great app!
thanks for this idea; I have so often wanted to erase comments from Turtle Boy and from Dr. Ed (the Talking Horse). they always comment on public education and will throw a ‘monkey wrench” into the discussion just to inflame things.
I understand your concern, since we see gerrymandering abused so badly in some states. However, if you look at the map and your goal is (a) to keep separate towns in a single district, like Brookline, Newton, etc. and to keep neighborhoods intact, and (b) since the city of Boston is too large and populated to be in one district, to distribute it so each district official has roughly the same number of citizens to represent, you have to make some strange boundaries. Brookline in particular makes it hard.
Try blocking out the separate cities and look at just the map of Boston. You can also access the census data at https://www.census.gov/ and look at what the feds provided to the states to work on redistricting. It’s truly not an easy process with the absolute best of intentions.
If you seriously look through and analyze all the data and have better suggestions, from what I know of Will, he’ll be happy to talk with you.
At least it does not have a big spur that extends down to Truro, Boston was in the past, considered the hub of the universe, so to maintain power, it always had it’s tentacles out to distant places
In case you are curious about what gerrymandering actually is (and this cannot be reasonably called gerrymandering):
https://en.wikipedia.org/wiki/Gerrymandering
https://ballotpedia.org/Redistricting_in_Massachusetts_after_the_2020_census
Dee, I absolutely agree with your comment. It is shocking to me that some people think that censoring comments they don’t like is something to be proud of. It shows inability or unwillingness to debate issues – a skill that citizens need in our public life more than ever if we’re to remain a democracy.
Will You have been an outstanding senator. I live in Back Bay and this indeed is very bad news for me
Thanks Will. It cannot have been easy – juggling the many goals inherent in any re-districting. Thanks for your work on this task! I noted that if the maps hold I would lose my current state senator, who I think is terrific. However, I would be represented by you – which would be great.
Same here. These maps are hard to read, though.
Will-
You have set a high bar with your professionalism and work ethic in the past and undoubtedly will do that
wherever you go.
Wishing you all the best!
Agreed.
I appreciate the transparency but the provided map is rather hard to interpret, especially with the overlapping boundaries. I hope something more accessible is available to all MA residents once this is rolled out.
Could you please post clearer pictures of your current and proposed districts. Each one separately, not on top of each other and without the lines of bordering districts in the pictures.
I agree. I found the map hard to understand.
I greatly appreciate your dedication and hard work on this, Will. And I agree with Sue and Ilana that the green lines are very hard to make out from other elements on the map and the overlap with the red doesn’t allow for easy comparison. Could the be visualization be tweaked a bit to make it clearer? Thank you.
I’ve added a couple of illustrations which may be more helpful. Of course, this highlights the problem — the existing lines are especially confusing.
Thank you very much. I still find them both confusing but these illustrations are more helpful. As always, you were very responsive to constituents’ requests and very quickly.
I know the many hours that you most likely have put into all of your choirs. Allston and Brighton contain an abundance of students, increasing the difficulty of verifying legitimate voters. The map hurts my eyes, sort of, difficult to really understand the total impact.
Thanks for all your hard work on this!
Being a resident in the Back Bay, I will miss your thoughtful presentations of the issues at hand and your willingness to hear us out. Your actions as our representative have helped me maintain faith in our democratic process. This is what democracy/representative government should be.
Also, what about having redistricting placed in the hands of an outside, (politically) independent body? This way legislators can not be accused of gerrymandering.
to hard to read map…..very confusing….live in back bay.south end to confusing to figure if I am one street away from the other district.
I think it would be easier to just divide it by towns then mess mash……….
Thanks for your work, Will. I find the maps confusing, too. Could someone use a light fill color with one map showing the old district, and another showing the new? That would be a lot easier to see than trying to follow the lines.
Cannot thank Will enough for all the selfless and hard work. It never made a lot of sense to me why Back Bay and Watertown would be in the same district but since my Congressional District runs from Everett down to Randolph I have pretty much given up on any of this making sense.
I may have to move so as to continue having you as my senator, but I agree: can’t the map use a light fill color with one map showing the old district, and another showing the new?
Is there a shaded polygon version of these maps (the current vs. the proposed & overlaid gradient) somewhere that’s easier to read? Can you please post the link to those shapefiles & layers, &/or have them put into a custom google map that shows these? Is this also changing the House Rep lines? If so, how? Do you have a map that shows the breakdown of how people voted, & is it proportionally representative in the proposed new redistricting so that the greater whole districting voting split is an accurate reflection of the voting split of the constituent parts? If not, how can the proposed map be readjusted to more accurately reflect that?
If MA lines are drawn based on metes & bounds, why is part of Cambridge included as part of the new area, yet not Brookline, even though Brookline is geographically in between Allston-Brighton & Fenway/Back Bay/South End?
Wouldn’t it make more sense to include all of a city/town together under the same unified representation districting, and not part (aside from Boston, which is large), especially when certain municipalities functionally have their own laws (ex: resident parking, overnight parking, snow parking, school districts, library systems with public internet & printing, community cooling centers, grocery bag mandates, who counts officially as a “family member” in in-patient medical settings & emergencies (specifically in Cambridge, which has official legislation on the books that is more broad & inclusive than elsewhere compared to most of the rest of the country when defining a “non-nuclear family”), taxes, etc.)?
If I’m looking at the new proposed map correctly (unsure), is it proposing splitting Cambridge (which has heavy subway and bus urban public transit) up into 3 separate districts, all of which include more dispersed, 3-digit bus areas (the ones that tend to run maybe once an hour, only during commuting times?), instead of just putting it all into 1 unified Cambridge district? How can the map be redrawn so that all of a city/town/neighborhood all has the same representation?
Does the new proposed map make it so that everyone who is in the same zipcode has the same representation? That would be great & helpful & probably more representative given that the Census can report down to the blockgroup level, and it’s the Census that is supposed to be the data source for the redistricting. It doesn’t make sense that there can be neighbors who live across the street who are considered in a different district, even though they have the same zipcode, same city/town, and in some cases, the same street name, with the only difference being if their address is an odd number or an even; they should have the same representation, especially given that functionally, they are following the same local laws, and presumably, any community concerns that they have, their immediate abutting neighbors likely share similar concerns as invested stakeholders.
From: https://polyamorylegal.org/cambridge
“Non-nuclear families—such as single parents supported by relatives, step-families, open adoption families, multi-generational families, multi-parent families, and polyamorous families—have changed the landscape of American society, and yet, many of these diverse family structures are not protected or recognized by the law,” said Alexander Chen, Founding Director of the Harvard Law School LGBTQ+ Advocacy Clinic. A 2015 Pew Research Study shows that less than half of U.S. children below age 18 live in a family with two married parents in their first marriage. That means that many children live in families that do not enjoy the same recognition, rights, and protections as in the past. ”
Aside from the proposed redistricting, what constitutes a “family” makes a big difference when it comes to federal laws, such as the Family Medical Leave Act (FMLA), & it’s currently very narrow definition of “family,” which in a lot of cases, particularly with certain racial/ethnic demographics where multigenerational families & neighbors or close friends reside together or in close proximity and share resources such as child & elder care (aunties, uncles, nieces, nephews, cousins, close family friends, etc.), is not inclusive. Those laws make a big difference when it comes to, among other things, caregiving and receiving medical services, especially in an emergent setting, especially in times of covid, especially with severe hospital visitation restrictions given the pandemic.
Cambridge is only the 2nd city in the entire country to have such a law on the books (the City of Somerville was the first, which, if I’m reading the proposed new map correctly, is all in one district – unsure?). At the very least, it should not be split up; all of the City of Cambridge should have the same representation.
Cambridge has been split among three Senate districts for a long time. (2011, see https://malegislature.gov/StateHouse/MediaGallery/Image/SenateStatewide.jpg)
My hometown’s population (20% larger than when I grew up there in the ’60s and ’70s, and back to 1950 density) is too large for a single Senate seat.
Shapefiles for the current districts can be found here: https://malegislature.gov/Redistricting/CurrentDistricts/Senate
The proposed districts’ shapefiles can be found here:
https://malegislature.gov/Redistricting/ProposedDistricts/Senate
thanks for keep your constituents informed. Since I live in Watertown, I would not expect to see any changes resulting from redistricting. Please let us know if this is incorrect.
Correct as to the Senate district. No change for Watertown.
Hi Bob,
There a change. If you are in District C, Precinct 9, then State Rep. Owens is no longer your representative. Will is still your State Senator however, and that is great!
You are the person who keeps my faith in government alive. Many thanks for all you do and will do for our state but I will deeply miss you as my senator.
Thank you so much, Kristin. It has been a privilege to work with you as well.
Will, Redistricting is an incredibly difficult challenge. Districts need to be compact, contiguous and have about the same population. They should respect both geographic, topographic and community lines and make sure that people with a shared interest are grouped together and can have a voice. It’s nearly impossible to make that happen in a way that satisfies everyone. I appreciate your work on this difficult issue especially because of your willingness to take on the task with the full measure of intelligence, diligence and transparency that you apply to all issues. Still, I have to note that some will always see gerrymandering in the end product. The most important advantage of a non-partisan redistricting commission is not that so much that it would produce “better” district lines but that it would result in more confidence in the integrity of the product by those who feel wronged by the result. Thank you for your taking on this challenge.
Some would have more confidence in a commission. Some less. Ultimately the proof is in the pudding in every cycle.
Thank you for your presentation. But redrawing districts for a political objective = gerrymandering = bad policy.
Not sure what part of the plan you are criticizing. We feel pretty good about it.
I am very disappointed to be losing you from the Back Bay district – although we dont always agree- I admire your professionalism and responsiveness.
Thanks so much, Rich.
Does staying engaged in Charlesgate and Fenway issues mean that you still represent us in that immediate area or are you just staying involved because of your concern and work ethic, which are outstanding? A street listing would be helpful. Thanks!
In the October 19, I keep all of Charlesgate and most of Fenway.
Yay!
They are confusing, but you will still be representing me, which is a good thing.
My father and stepmother, who live in Neighborhood 9 Cambridge (where I grew up) will retain their current State Senator.
I will have all of Ward 9 in Cambridge in the new map.
Thank you for keeping us informed and soliciting input.
I plan to look more closely at the proposed boundaries before commenting on the plan, but would like to add an additional comment to those above regarding readability of graphic. For accessibility purposes it would be helpful to avoid red/green combination. These choices make it difficult for those with color blindness.
Thanks, Will,for the update. I hope that once again you will represent my area in W. Cambridge.
I can’t read the tiny maps with multiple green lines shooting off the graphic. It’s confusing and non-informative. Is there something you don’t want us to know?
I have lived in A/B for more than 40 years and have never heard of “North Allston”. Do you mean lower Allston? HarCo (Harvard Corp owned land)?
Hope the new map is more legible.
It is. Thank you!
I feel so fortunate to be represented by you in the state senate Will – really smart, always transparent and informative and communicative. Thank you.
We should add an overlay district for you including all of Walden Pond and the parking lots. You can give away some of the People’s Republic in exchange.
Would love to have Walden in my backyard.
not in your district any more sad
TBH, I don’t see how the East Fens has issues and interests in common with Winthrop and Revere. I want you to stay our senator, too.
So sorry that our corner of the East Fenway is no longer in your district. Please run for statewide office so I can vote for you again.
All I care about is how fairly the new lines are drawn, so that each district is as competitive as humanly (not partisanly) possible. Having a penchant for fresh 3rd party candidates, I feel that a really fair district map would give outsider parties a chance to bargain with the 2 entrenched parties, playing off each against the other…. in order to persuade 1 of them to support a couple of popular policies that might not be favored at the outset by either major party. The result, in the best of all political worlds, could be an informal provisional coalition that would get at least a couple of good innovative policies (enjoying lots of grassroots support) passed in the new legislature. I know, I know: “Dream on, dumb idealist! We old pros are a lot smarter than you think! Also better funded. And the local media are on first-name terms with all of us! So just bend over and…ahem!…kiss our, ah, ring.”
Partisanship isn’t much of an issue in Massachusetts redistricting. Most districts do lean Democratic.
Quite right. I keep forgetting that I live in Massachusetts. Where the best chance a Republican appears to have of getting elected is to make sure there’s a “D” beside his/her name on the ballot. If only more of them would sail under their true colors!
What additional areas did senator DiDominico pick up? Thanks